Home

Transformer整体框架

  • 和其他人工智能整体框架一样，Transformer也是一个黑盒(black-box)。
  • $输入\Longrightarrow 处理输入\Longrightarrow 输出$

宏观理解

  • 将TRANSFORMER放大看，可以看到TRANSFORMER是由编码组件(encoders)和解码组件(decoders)两部分组成

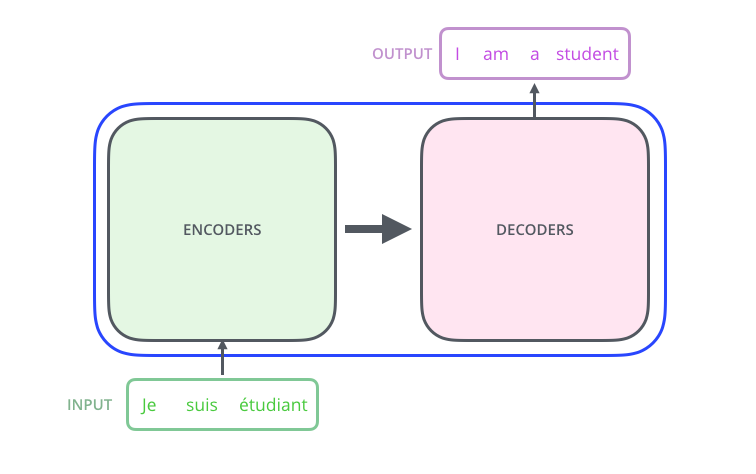
encoders & decoders

  • 在放大看，可以发现编码组件encoders和解码组件decoders是由若干编码器encoder和解码器decoder组成。在Attention Is All You Need中，编码器和解码器的数目为6个($N\times$中的$N$为这里的个数)。当然，这个数目可以改变，只要训练出来模型的效果好就行

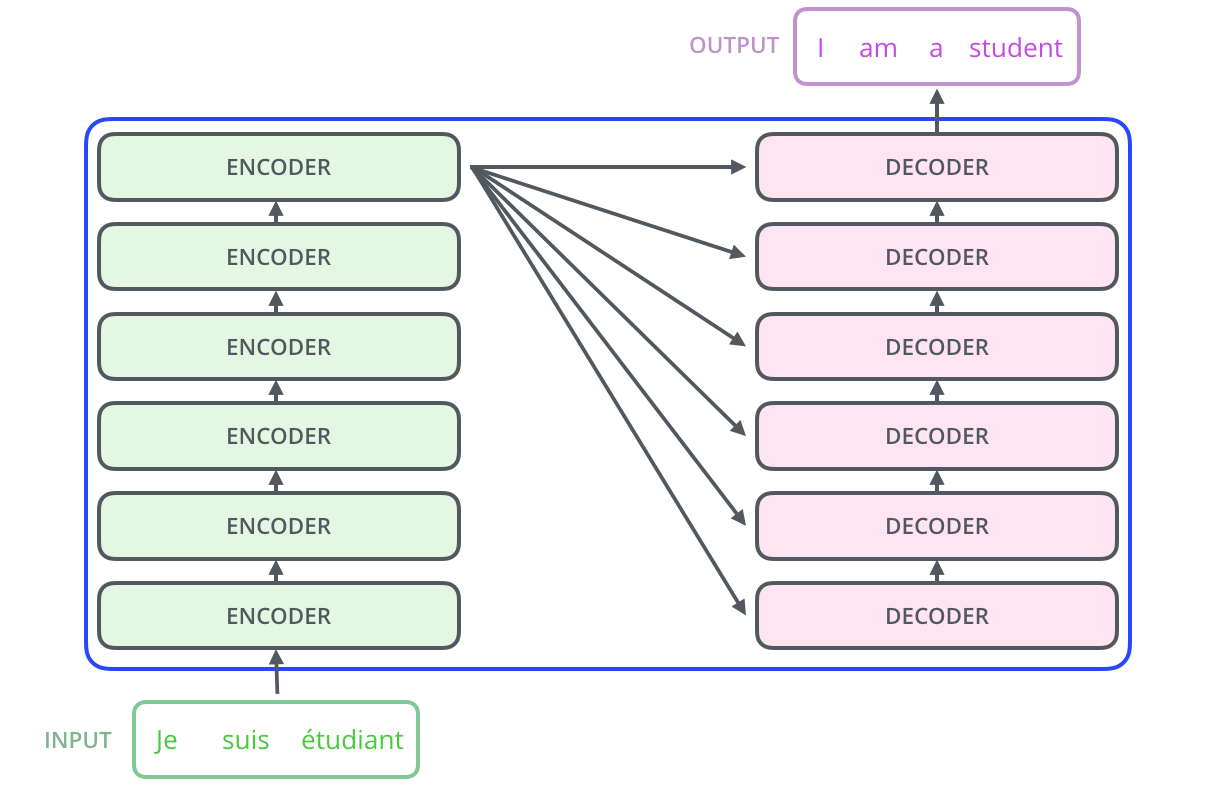
encoder && decoder

  • 注意：编码器和解码器在结构上是相同的，但是并没有共享参数
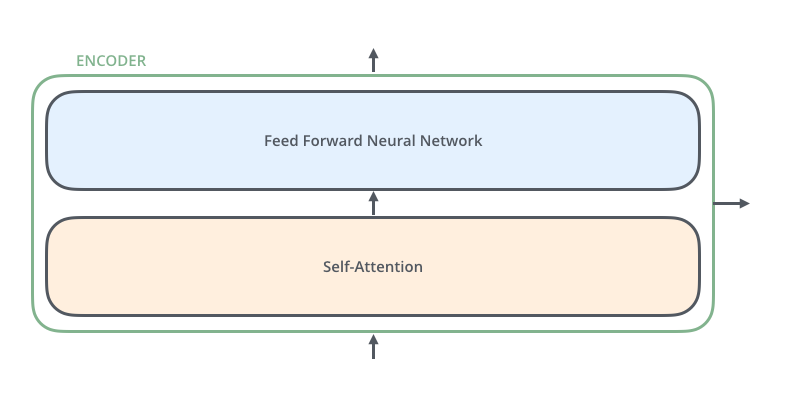
  • 继续放大看编码器，可以发现其是由自注意力层Self-Attention和前馈神经网络层Feed Forward Neutal Network组成

encoder

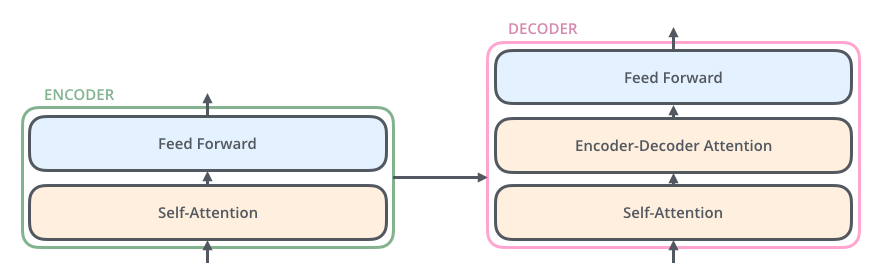
  • 与编码器不同的是，解码器在Self-Attention和Feed Forward Neural Network之间加入了Encoder-Decoder Attention层

encoder && decoder

Transformer结构细节

词编码(Word Embedding)

  • 常用的词编码，如One-Hot编码，有诸多缺点，如无法表达两个单词之间的相关性（距离）
  • 比如，我们有四个词(dog, apple, banana, cat)使用词编码
1
2
3
4
dog:    [1, 0, 0, 0]
apple:  [0, 1, 0, 0]
banana: [0, 0, 1, 0]
cat:    [0, 0, 0, 1]
  • 这种方法编码简单，但是他无法从向量上反映两个词之间的相关性
  • 比如在人类看来，dog和cat属于同一类事务，apple和banana属于同一类事务。apple距离banana的距离要比dog更近，但是在one-hot编码中他们的距离是一样的
  • 另一个弊端是词向量维度过大，编码的向量维度等于单词的个数

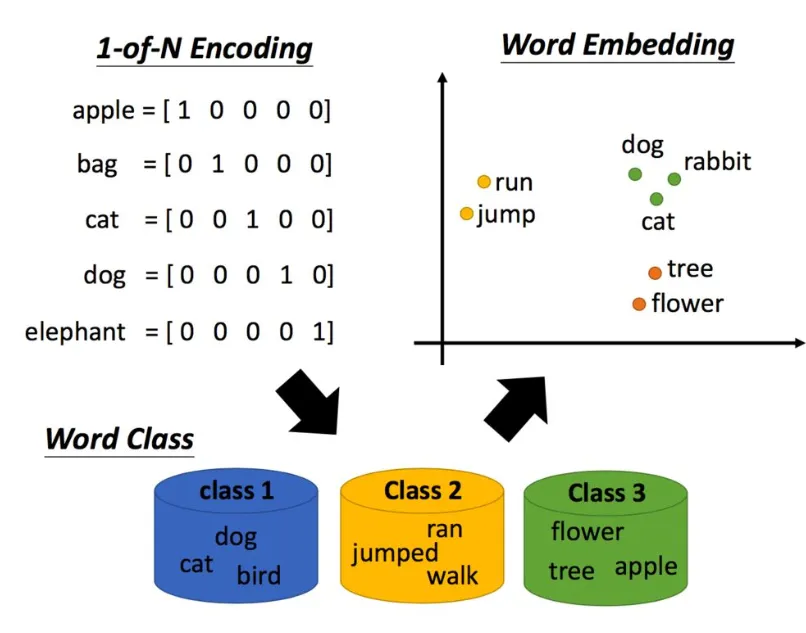
Word Embedding

  • 通过词编码Word Embedding即可很好的反映出同一类词的相关性（距离）

位置编码(Positional Encoding)

  • 位置编码的作用是对一个句子中每个单词贴上标签，表明他们在句子中的位置(1, 2, 3, 4, …)
  • 当然，具体操作肯定不是简单的把1, 2, 3, 4代入

$$
PE_{(pos, 2i)}=sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}})\
PE_{(pos, 2i+1)}=cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})
$$

举个栗子🌰

  • 对于句子：Dumpling is handsome
    • 句子长度n为3
    • 令词嵌入Word Embedding维度$d_{model}$为4
    • 整个句子是$n \times d_{model}$即$3 \times 4$维矩阵
    • $0\le i \lt \frac{d_{model}}{2}$
    • 对于$Dumpling$，其$pos=0$
    • 故其位置编码为$[PE(1, 0), PE(0, 1), PE(0, 2), PE(0, 3)]$即$[sin(\frac{0}{10000^{\frac{0}{4}}}),cos(\frac{0}{10000^{\frac{0}{4}}}), sin(\frac{0}{10000^{\frac{2}{4}}}), cos(\frac{0}{10000^{\frac{2}{4}}})]$
    • 依次类推，即可得到该句子的位置编码

数学原理

  • 为什么用三角函数，为什么偶数维（2i）用sin，奇数维（2i+1）用cos？

    • 由三角函数性质公式

    $$
    sin(\alpha+\beta)=sin\alpha cos\beta + cos\alpha sin\beta\
    cos(\alpha + \beta)=cos\alpha cos\beta - sin\alpha sin\beta
    $$

    • 故有

    $$
    PE_{(M+N, 2i)}=PE_{(M, 2i)}\times PE_{(N, 2i+1)} + PE_{(M, 2i+1)}\times PE_{(N,2i)}\
    PE_{(M+N, 2i+1)}=PE_{(M, 2i+1)}\times PE_{(N, 2i+1)}-PE_{(M,2i)} \times PE_{(N,2i)}
    $$

    • 也就是说，$PE_{(M+N)}$可有$PE_{(M)}$和$PE_{(N)}$相互计算得到，也就是说：绝对位置编码中包含了相对位置的信息。

编码器