使用线性模型有很多缺点,比如Model Bias(模型偏差)
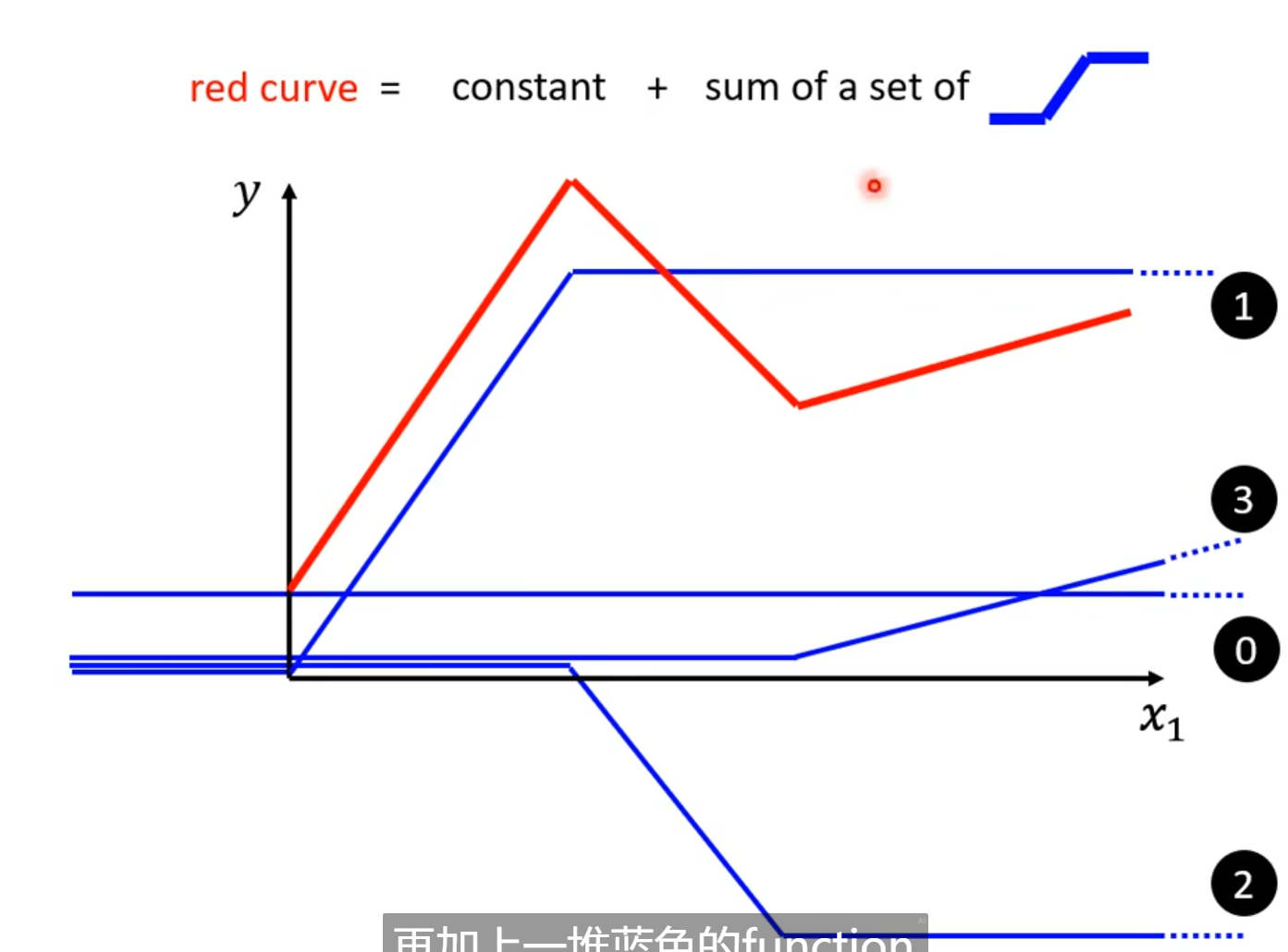
红色的曲线可以表示为一系列蓝色曲线的和
对于连续曲线函数,可以用一条分段线性函数来近似。为了有好的相似,我们需要足够多的片段
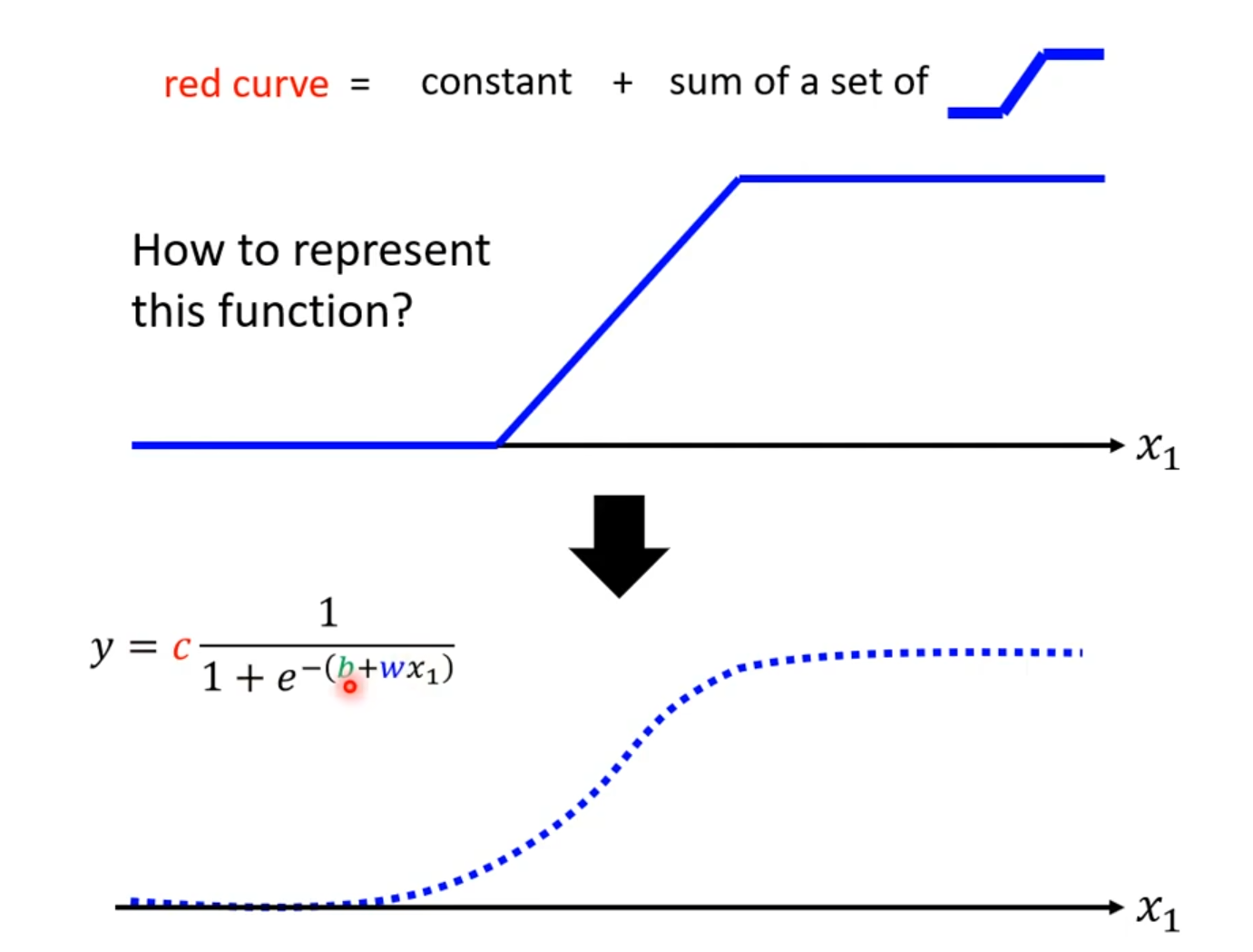
我们可以用sigmoid函数来近似表示分段函数
$$
y,=,c \frac{1}{1,+,e^{-(b+wx_1)}}
$$
也就是说,对于蓝色的曲线,我们有:
$$
曲线1:c_1sigmoid(b_1,+,w_1x_1)
$$
$$
曲线2:c_2sigmoid(b_2,+,w_2x_2)
$$
$$
…
$$
$$
曲线i: c_isigmoid(b_i,+,w_ix_i)
$$
因此,对于红色的曲线则有
$$
y,=,b,+,\sum_i c_isigmoid(b_i,+,w_ix_i)
$$
$w_{ij}$: 对于第$i$个$Sigmoid$函数来说,$x_j$的权重 。
对于:
$$
y,=,b,+,\sum_i c_isigmoid(b_i,+\sum_j,w_{ij}x_i)
$$
$i:1, 2, 3$: no. of sigmoid
$j: 1, 2,3$: no. of features
(说实话第一次看见这个公式的时候还是比较懵的,之后通过一个具体的例子了解了这个公式)
对于机器学习公式的例子
$$
r_1,=,b_1,+,w_{11}x_1,+,w_{12}x_2,+,w_{13}x_3
$$
$$
r_2,=,b_2,+,w_{21}x_1,+,w_{22}x_2,+,w_{23}x_3
$$
$$
r_3,=,b_3,+,w_{31}x_1,+,w_{32}x_2,+,w_{33}x_3
$$
也即
$$
\begin{bmatrix}
r_1\
r_2\
r_3
\end{bmatrix}=\begin{bmatrix}
b_1\
b_2\
b_3
\end{bmatrix}+
\begin{bmatrix}
w_{11} & w_{12} & w_{13}\
w_{21} & w_{22} & w_{23}\
w_{31} & w_{32} & w_{33}
\end{bmatrix}
\begin{bmatrix}
x_1\
x_2\
x_3
\end{bmatrix}
$$
故有
$$
\mathbf{r},=,\mathbf{b},+,W,\mathbf{x}
$$
不妨设$\mathbf{a}=\sigma{(r)}$
则有$y,=,b,+,\mathbf{c}^T\mathbf{a}$